How to Learn Data Science and Probability in 2021

I recently graduated from Chemical Engineering and landed my first role as a data analyst in a tech company. As I was preparing for a role in data, I needed to find resources to learn data science and probability. It’s not surprising that I have received questions like…

‘How did you learn the skills of a data scientist yourself?’

It is not easy, but it is definitely doable. It’s not easy to find the best resources out of the sea of resources on the internet.Thus, in this post, I will share my favorite resources I used in learning probability for data science.

But before that, let’s understand…

What is data science?

Fact is, different companies define data science differently, making the term ambiguous and somewhat elusive. Some say that it is programming, others contend that it’s mathematics, while others say it is about understanding the data. Turns out, they’re all somewhat correct. To me, the definition that I agree most is this —

Data science is the inter-disciplinary field that uses techniques and theories drawn from the fields of mathematics, computer science, domain knowledge. [1]

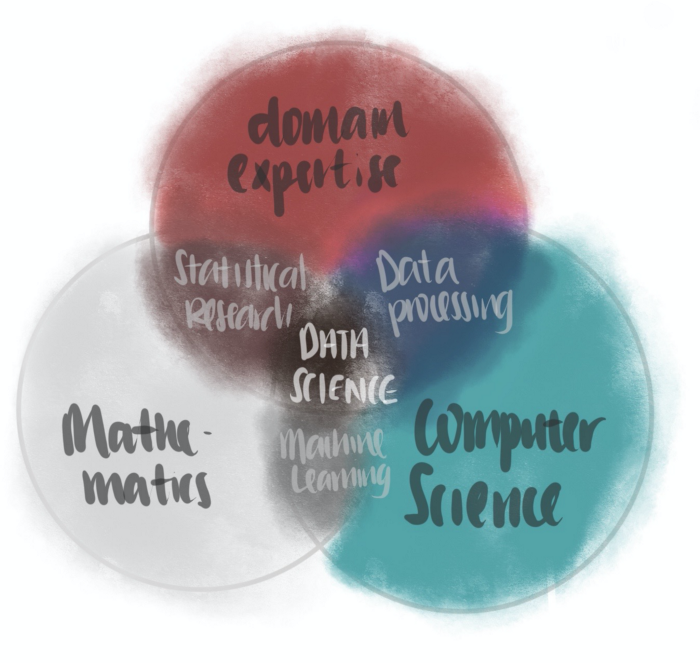
In this post, I will highlight how I learnt about the ‘Statistical Research’ knowledge required of a data scientist by learning probability. To do so, one needs a firm understanding of the theory of probability.

Okay, so how do I learn probability for data science?

Probability is not the easiest topic to master as its theoretical nuances can be esoteric and arguably obscure. But it need not be difficult — the best resources that I share below shy away from jargon and instead teach probability intuitively.

Disclaimer: I do not receive any compensation for promoting any content in this post.

Theoretical Lecture Series

The following three are excellent lecture series by reputable organizations on probability. Since the content of the three series is largely similar, I suggest you opt for one of lecture series and follow through.

• Khan Academy’s Statistics and Probability (High school level)
• HarvardX Stat 110: Introduction to Probability (College / Graduate level)
• MITx 6.431 Probability — The Science of Uncertainty and Data (College / Graduate Level)

Application Lecture Series (Optional)

The above lecture series does not teach you how to solve probability problems using programming languages like R or python. The following lecture series will allow teach you the coding aspect of probability. If you are already familiar with python or R, it is easy to pick up the syntax required to solve probability problem without having to attend a class.

However, if you feel more comfortable having some guidance through a class, here are my recommendations. Again, since the content of the series issimilar, I suggest you opt for one of the following.

• HarvardX Data Science: Probability on EdX (R)
• HarvardX Data Science: Probability on DataCamp (Python)
• Duke University’s Introduction to Probability and Data with R on Coursera

Books (Optional)

As I was going through the lecture series, I found myself requiring some additional help from textbooks. I found the following introductory textbooks particularly enlightening.

• Introduction to Probability by Blitztein and Hwang, used as a companion text to Harvard Stat 110. Available free here.
• Introduction to Probability by Grinstead and Snell, used as a companion text in Dartmouth College. Available free here.
• Introduction to Probability by Bertsekas and Tsitsiklis, used as a companion text for MITx 6.431. Available on Amazon here.
• (Some chapters in) Applied Statistics with R, used as a companion text for STAT 420 at the University of Illinois at Urbana-Champaign. Available for free here.

Videos (Optional)

I also consult videos on an ad-hoc basis on certain concepts that I am not too clear with. Here I list some of my most frequently used (free!) video resources which explain concepts clearly and concisely.

• StatQuest with John Starmer on YouTube
• Discrete Math Series by Dr Trefor Bazett on YouTube (containing concepts in probability)

Websites (Optional)

• Sometimes, it might be hard to visualize certain concepts in probability. To address that, the Seeing Theory providing a stunning interactive experience in visualizing probability concepts.

That’s a lot to choose from. How do I pick the best one?

My suggestion is to follow through a lecture series of your choice, whether it is from Khan Academy, HarvardX or MITx. Along the way, you can read the textbook to strengthen your understanding of the topic and work on the examples provided in the book.

If you have any doubts from the lecture series and the textbook, the videos and the websites provide excellent alternative explanations that might help you understand the topic.

I used MITx 6.431 the most extensively. Along the way, I consulted materials from Khan Academy and Harvard Stat 100 occasionally. Therefore I personally recommend aspiring data scientists to pursue MITx 6.431.

6.431x gives the MIT rigor

The online class is taught at a similar pace and level of rigor as an on-campus course at MIT by the same lecturer, Prof Tsitsiklis. In fact, MITx 6.431 has an on-campus version of MIT 6.431 on MIT Open Courseware.

MITx is superior (in my opinion) to the version on Open Courseware because simply because MITx is designed specifically for online delivery while the version on MIT Open Courseware is a series in-person lecture recording.

6.431x has an awesome teaching team and materials

Prof Tsitsiklis avoids technical jargons and elucidates concepts plainly. Moreover, the teaching assistants who guide students through the recitations and tutorials are great at providing clear explanations of challenging problems. The teaching team also made sure that the content is also logically ordered and concisely summarized. The process of learning was made rather frictionless and pleasant by the teaching team.

6.431x might help with graduate school

For those considering a graduate program, MITx is an excellent choice. 6.431x is part of the MIT MicroMasters Program in Statistics and Data Science. This MicroMasters Program consists of 4 core courses (on probability, machine learning, statistics and a capstone exam) and 2 electives (on data analysis).

Upon completion of the MicroMasters program, one has the opportunity to apply for MIT’s PhD in Social & Engineering Systems. Apart from that, it offers a pathway to graduate programs in Curtin University, Harvard Extension School and Tsinghua University, among others.

You can try it out first.

You can attend the first few weeks of lecture on EdX for free and decide if you like it before attending.

So, what do I need to learn in probability?

Each of these courses has slightly different scopes. However, in general, they are excellent starting points should master the following if you were to learn probability.

Here are some topics that a data scientist should master in probability. I will illustrate each topic with a related question.

The concept of ‘independent events’

Today the sun rose. Will the sun rise tomorrow?

Put plainly, if two events are independent, the two events do not affect each other in any way. For instance, we know for a fact that sunrises are independent of one another. This is because knowing if the sun rose today doesn’t tell us any additional information on whether the sun is rising tomorrow.

The concept of independence is a cornerstone to probability and statistics as it is an assumption made in many probability concepts and statistical models. It is crucial to learn the mathematical intuition of independence to master the probability concepts later.

The Counting Rule

What is the probability that a 4-number password has repeated numbers if only numbers are used?

To solve this problem, we need to count the number of passwords that can be formed with and without repeated letters. In general, we can know the probability of an event if we can count the number of ways different events occur. If you’ve found the answer, comment down below.

Discrete random variables

If we flip a fair coin by 6 times, how many times do we expect to see a head?

To answer that question, we can to model a coin flip as a discrete event i.e. an event with only two possible outcomes (as opposed to having infinite possible outcomes). In other words, we are modeling each coin flip as a discrete random variable, called a Bernoulli random variable.

If we treat a head as 1 and a tail as 0, we can sum up the results of 6 coin flips to get another discrete random variable (a Binomial random variable).

The number of times we see heads will simply be the expectation of the binomial random variable.

Continuous random variables

What is the price of a Tesla given that its a 5-year-old series X?

To answer this question, we can model the price of 5-year-old Series X Tesla as a normal random variable. This means to say that most 5-year-old Series X has an average price. Some cars are more expensive than the average price while some less expensive than the average price. However, it is unlikely to find cars which much, much are pricier or cheaper from the average price.

In other words, the price of a 5-year-old series X can be modelled as a bell shape distribution.

In fact, we can build a linear regression machine learning model that predicts the price of a Tesla given its age and model. When we do that, we are implicitly modelling the price of a Tesla as a normal random variable!

Bayesian inference

Say if we flip a coin 10 times. We do not know anything about this coin, so we initially assume that it is a fair coin. If the coin shows heads 9 times, what is the probability that the coin is fair?

Bayesian inference is a burgeoning field and is rapidly gaining importance in data science. Bayesian inference is simply the principle of updating the probability of an event based on what we see as more information becomes available. [2]

Let’s apply the principle of Bayesian inference in this case. Having observed the coin showing 9 heads out of 10 tosses, there is a high probability that the coin is biased towards heads though we initially assume that it is fair.

An application of Bayesian inference in machine learning is the Naive Bayes classifier. For instance, a Naive Bayes classifier may be used to classify whether an email is spam or otherwise. Initially, the model may assume that all emails are not spam. It then updates its belief based on the email address of the sender and the content of the email.

Limit theorems

What is the proportion of observing a head if I were to toss a fair coin 4 times, 400 times, 40000 times, or 4,000,000 times?

If we were to toss the fair coin 4 times, you wouldn’t be surprised if all 4 times are all heads. If we were to toss the fair coin 4 million times, we would be extremely surprised if all tosses come up to be heads.

Why is this the case? This is because we instinctively believe in the law of large numbers. Colloquially, the law of large number says if we perform the same experiment over and over again, the average of the results will become closer and closer to the truth (the expected value).

Limit theorems such as the law of large numbers are important in analyzing large data sets by machine learning systems.

Classical Statistics

After conducting a presidential election poll involving 100 Americans, how confident are we in predicting the victory of Trump or Biden?

This would depends on concepts like p-value and confidence intervals, both of which are crucial parts of classical statistics that are commonplace in data science interviews.

Why is Probability Important to Data Science?

Probability is the bedfellow of statistics

The field of data science often leverages statistical tools to make inferences or predictions. To understand such statistical tools thoroughly, one needs to build a strong foundation in probability.

For instance, a data scientist in Facebook may need to plan an A/B test Facebook users to determine if a user clicks on a new button. In the planning of the experiment, one needs to form hypotheses and draw up an appropriate sampling plan before running the experiment. A data scientist must understand probability concepts before making a proper sampling plan. Only then can statistically significant inference be made about Facebook users in general.

Probability forms the foundation of machine learning

Moreover, unbeknownst to many aspiring data scientists, the concept of probability is also important in mastering concepts machine learning. Many machine learning models are built on the assumption that the data follows a particular type of distribution.

Without understanding probability, a data scientist will not be able to decide if the data fulfils the assumption of the machine learning model and therefore might not make the best choice in the machine learning model.

For instance, a linear regression model assumes that the noise of each data point follows a normal distribution. To understand what means, a data scientist should know what a normal distribution is — which is what you learn in probability.

Where to Go Next

After learning the theoretical aspect of probability, you can

• apply the probability concepts using R or Python in a project.
• take a class in A/B testing, an important skill for a data scientist.
• learn more about statistics (in the next blog post, I will highlight what are the key differences between probability and statistics, and share some resources for statistics.)

This is a 5-part blog post to learning data science. If you’ve enjoyed this and would like to become a data scientist, feel free to follow this series:

• Part 1 — Data Processing with SQL, Python and R
• Part 2 — Mathematics, Probability and Statistics (you’re here!)
• Part 3 — Computer Science Fundamentals (coming soon)
• Part 4 — Machine Learning
• Part 5 — Building your first Machine Learning Project

Other Readings

If you enjoyed this blog post, feel free to read my other articles on Machine Learning:

• How to be a Data Analyst — Data Viz with Google Data Studio
• 4 Steps to be a Great Data Analyst — Don’t be a Query Monkey

Conclusion

Learning these resources made me much more confident in data science as they provided me with a great foundation to learn other machine learning and data science concepts.

All the best to your learning journey! Feel free to reach out to me via LinkedIn for any suggestions or questions.

References

[1] Dhar, V. (2013). “Data science and prediction”. Communications of the ACM. 56 (12): 64–73. doi:10.1145/2500499. S2CID 6107147. Archived from the original on 9 November 2014. Retrieved 2 September 2015.

[2] “Bayes’ Theorem (Stanford Encyclopedia of Philosophy)”. Plato.stanford.edu. Retrieved 2014–01–05.